Introduction
Micro Maths is a complete self-tuition and revision course taking beginners up to GCSE standard. It is designed to be used both in schools and homes.
Computer program loading instructions are given in Appendix 1.
There are two discs (or equivalent) used in the course: disc 1 and disc 2. In order to run the program you first load the "menu" and choose from the list of topics by pressing the appropriate letter.
First, read the section appropriate to your computer in Appendix 1. This will show you how to load the computer programs into your computer and how to use the program.
To help you find the appropriate program, the disc number (or disc side number) and program letter is given. Different versions have different programs but they are all listed below.
MICRO MATHS 1
Percentages
OPTION A(1)
In this program a proportion of a wall, centipede or building is coloured in. It can be seen from this how, for example, 50 out of 100 is the same as a half (1/2) as the picture is made up of 100 equal parts. When converting fractions to percentages, ideally write the answer to two decimal places. When converting percentages to fractions, use the / symbol when keying in fractions, e.g. 2/3. Remember to omit any unnecessary spaces.
Averages and Histograms
OPTION B(1) It covers histograms and means (averages). Histograms are charts consisting of long, thin bars (or rectangles) drawn side by side. The height (or length) of each bar is the number of occurrences of the condition represented by that bar.
Ratio and Proportion
OPTION C(1) Use the symbol / when expressing one value as a proportion of another value.
Number
OPTION D(1) Your version of Micro Maths may have either this or the following program, or both. This program covers recognition of odd and even numbers, squares, factors and square roots of numbers.
Changing The Bases of Numbers
OPTION D(1) or L(1) A value can be expressed in hundreds, tens and units (Denary), or in groups of 1, 2, 4, 8 etc (binary) or groups of 1, 8 (8 x 8) (octal etc). For example, twelve can be written as 1 group of tens and 2 groups of ones (i.e. 12) or 1 group of eights, 1 group of fours, 0 twos and 0 ones (1100), or a 1 eight and 4 ones (14). This is shown in the program by a diagram of bricks. This program includes the conversion of denary numbers to binary and octal numbers to denary.
Mensuration
OPTION E(1)
Your version may have either this or the following program, or both. This program covers the perimeter and area of squares, rectangles and triangles. The diagrams of squares and rectangles show how if the shape is divided into squares of a centimetre width and height, then the area of the shape is the total number of centimetre squares. The diagrams of triangles show how as a triangle is made up of two half rectangles, so the area of a triangle is half the area of the equivalent rectangles.
Operations on Numbers in Different Bases
OPTION E(1) OR M(1) It covers binary addition, octal subtraction and binary multiplication. If you cannot work out the answer in your head, you may enter the Calculator mode and calculate the result of each pair of digits, going from right to left.
Polygon Properties
OPTION F(1) This covers the calculation of the sum of the interior angles of a polygon and the value of any angle in a regular polygon. A five-sided polygon with interior angles marked is shown in Appendix 1.
Solution of Agebraic Equations
OPTION G(1) This teaces the solution of equations by addition, subtraction, multiplication or division.
Simplification of bracketed quantites in Algebra
OPTION H(1) This involves multiplying an expression by a constant, and also by another expression.
Simple And Compound Interest
OPTION I(1) In the forumalae given, the letters have the following meaning:
| P | is the principal, that is the amount of money lent |
| T | is the time in years for which the money is lent | R | is the rate of interest in percent per annum | I1 & I2 | are the interest paid in the first and second years respectively | I | is the total compound interest |
Solution of Triangles Using Sine and Cosine Formulae
OPTION J(1) This covers the solution for either acute or obtuse angled triangles. The notation used is that the length of a side has a lower case letter, which the corner opposite has a capital letter. See Appendix 1.
Profit And Loss
OPTION K(1) This shows how percentages are used in profit and loss calculations.
MICRO MATHS 2
Triangles
OPTION A(2)
The computer program covers both the identification of similar triangles and problems using them. In the identification section you are given details of two triangles, ABC and PQR, and asked if they are similar. You must answer Y or N (for Yes or No respectively). The section section sets problems on similar triangles.
Geometry of the circle and its chords
OPTION B(2)
This teaches and tests you on circle theorems. In the diagram OP is at right-angles to BD, and OQ is at right-angles to AD.
Advanced Statistics
OPTION C(2)
It covers Pie Charts, modes and medians. The Pie Chart used is shown in Appendix 1 and you are required to find the angle marked.
Applications of Pythagoras' Theorem
OPTION D(2)
This covers the application of this theorem to right-anged and isosceles triangles., Isoceles triangles have two sides of equal length (AB = AC in diagrams below). Any line drawn from A to BC, that is at right angles to BC, bisects BC (i.e. cuts BC in half).
Trigonometry
OPTION E(2)
This teaches and tests elementary trigonometry using the sine, cosine and tangent rules.
Factorisation of Algebraic Equations
OPTION F(2)
Two types of equations are used: standard, quadratic and those solved by the "difference of two squares" method.
Graphs
OPTION G(2)
This is on calculating the values needed to draw graphs.
Simulatenous Equations
OPTION H(2)
In these problems, capital X represents the letter Z, while "x" represents the multiplication sign. The value of X and Y for each problem must be keyed in, in turn, separated by one space. Remember 2 - - 1 = 2 + 1.
Indices
OPTION I(2) and J(2)
Both these programs are on indices. The answers to the problems on zero and fractional indices are numbers, while the answers to the problems on negative indices must always be expressed in terms of Y.
Vectors
OPTION K(2)
To key in a vector, normally first key in a left-hand bracket. This is immediately followed by a number and a right-hand bracket, then press RETURN. Now key in the second row of the vector in the same way, followed by RETURN. The calculation mode may only be entered before keying in the complete vector, not half-way thourgh.
Vectors are values which have both size and direction, such as velocity (speed in a particular direction). Diagrams of the vectors of the problem are shown after the complete explanation. In these the end of each vector is lebelled. It can be seen in the diagrams of the multiplication problems that if the vector U is multiplied by 3, say, its length will be multiplied by 3, but the direction stays the same. In the diagrams for the addition problems, the unmarked vector is vector U + V.
Matrices
OPTION L(2)
Matrices are normally keyed in the same way as vectors, except each element of the matrix (number) is separated from the next by a space. Again, the calculator mode can only be entered before keying in the complete matrix. For Commodore 64, see Appendix 1.
Probability
OPTION M(2)
Your version may have either this or the following program, or both. This covers probability calculations involving only one event and the answer can be expressed as a simple fration, not necessarily in its lowest terms. Also it includes the calculation of combined probabilities for independent events. The answers must be expressed as a fraction using the / sumbol, e.g. 1/3.
Differential Calculus
OPTION M(2) or OPTION N(1)
This is usually the final program and when you have completed this you have finished the course. Now I suggest you go through any topics again you had difficulty with. Then when you are happy with all the topics, attempt the papers from the book.
Software copyright (c) LCL G Ludinski Bsc (Hons) AMBCS AMIEE
Appendix 1
This covers the computer program loading instructions and how to use the programs.
Operating Instructions
Each program first asks your name, then sets you a problem.
If the answer is a number, omit any units, e.g. key in 4 not 4cm. Answers are normally considered crrect if they are within 0.1 of the calculated answer. If the answer is alphanumeric, i.e. a mixture of letters and numbers, then omit any unnecessary spaces, brackets, addition signs and zeroes preceding whole numbers. For example, key in X+2 not (+X+02). Use the up cursor (or ^) to represent "to the power of" e.g. X ^ 2 is X squared.
Remember, throughout all these problems to press RETURN after keying in the required response. If you have no idea of what the required response should be then just press RETURN on its own.
The correct response for some of the problems in the programs on the Vectors and Matrices takes up two screen lines. In this case, key in each line separately pressing RETURN after each line. If you have no idea of what the response should be then press RETURN twice.
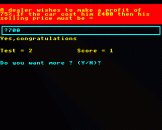
If you get the answer "Yes, congratulations" is displayed and then you are asked "Do you want more? (Y/N)". If you then press Y (RETURN) another program is displayed. If you press N, the program ends. Then, on the disc version, the menu is loaded again. In some versions you have the option of repeating the calculation by pressing R.
If you get the answer wrong, you are given a hint or some Maths instruction and then are told to try again. If you get it right this time, the program proceeds as described above. If not, the correct answer is given, followed by a complete explanation. Then the program proceeds as described aboe.
Loading Instructions
For the BBC put the tape or disc your require into the computer and then key in CHAIN "MENU" followed by pressing the RETURN key. Else "boot" the disc by holding down the SHIFT key and press and release the BREAK key. For BBC Master, CHAIN the CONVERT program from your 'Welcome' disc before loading Micro Maths, then hold down "A" while "booting".
Calculator Mode
If you require a calculator to calculate the result of a problem then press ? (RETURN) to enter the Calculator, for example, to add numbers 12 and 39 just key in:
12 + 39 =
+ - * (multiply) / (divide) ^ (to the power of) SQR (square root of)
The Trigonometry functions of 10 degrees, say, are:
SIN RAD (10), COS RAD (10), DEG ATN (0.1)
DEG ATN (0.1) stands for arc-tan with the result in degrees.
Brackets may also be used. As in a calculator, key in AC to clear the calculator display and key in = to display the result. No answer is displayed if you have made any typing errors. To exit the Calculator mode key in ? again.